tree是一种致力于提高索引效率加快存取速度二叉查找树[Binary Search Tree]形数据结构。

Binary Search Tree

先说一下二叉查找树[Binary Search Tree]，这是一个非常经典且查询效率很高的数据结构[如下图]，它有三个特性：

An Example of Binary Search Tree

  1. 每个节点[除叶子节点外]最多只有两个子树。

  2. 左子树的值都小于父节点，右子树的值大于父节点，也就意味着父节点的值介于左子树和右子树之间。

  3. 在n个节点中找到目标值，一般只需要log(n)次比较。因为每一次只需要搜索一个子树。

但是这种索引结构并不适合数据库系统，因为根据第三个特性，运算的复杂度跟树的层数相关，在最差情况下，在n层的树种，一个数据需要比较n次才能找到。对于数据库来说每进入一层就要进行一次I/O操作，非常耗时，因为硬盘的读写时间远远大于数据处理时间。所以为了进一步适应数据库的情况，才有了B tree。

B Tree

B tree的核心设计思想就是，减少层数以便降低I/O开销，一次性的尽可能多的读取数据，例如下图，最多的节点可以包含4个数据。

An Example of B Tree

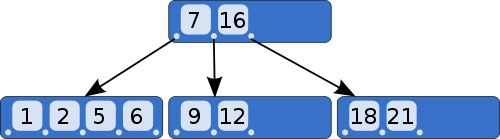
对应于二叉查找树，B tree也具有三个特点。

  1. B tree的每个节点可以包含多个值。

  2. B tree只会在当前层所有节点都已经满了的情况下才会创建新层，不然就会一直向当前层的节点添加数据。

  3. 父节点的数值个数和子节点的个数有严格的对应关系。如果父节点有x个值，那么此父节点一定具有x+1个子节点。比如上图中的父节点，有7和16，那么父节点就有且只有3个，第一个节点的所有数值均小于7，第二个节点内所有数值均大于7且小于16，而第三个节点内所有值必须大于16。

这种数据结构，非常有利于减少读取硬盘的次数。 假定一个节点可以容纳100个值，那么3层的B树可以容纳100万个数据，如果换成二叉查找树，则需要20层！假定操作系统一次读取一个节点，并且根节点保留在内存中，那么B树在100万个数据中查找目标值，只需要读取两次硬盘。

B Tree

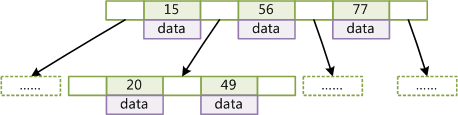
所以B tree适合的应用场景在于I/O操作耗时长，但是一旦读取之后处理速度非常快。