本年介绍了作为强化学习基础的Markov Decision Process，可以帮助理解比较重要但容易忽略的知识。

Background

下图通过抽象的描述了一个Agent-Environment的大致流程[MDP和RL都是基于这样的流程]。值得注意的是$[\mathcal{S},\mathcal{A},\mathcal{R}]$和$t$顺序，$R_{t+1}$其实是根据$S_t$获得的奖励。

Agent-Environment Interface

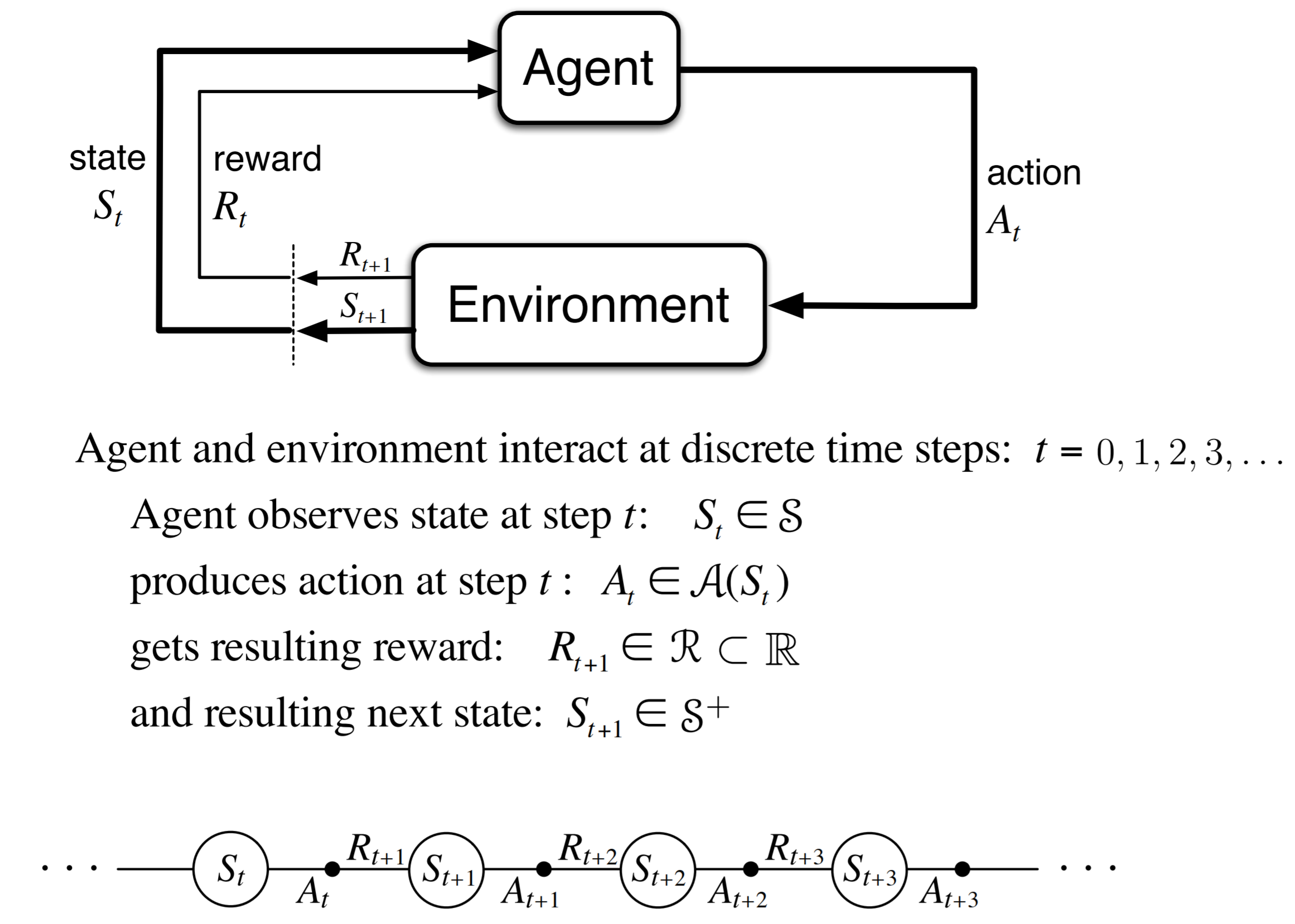
Markov Property

马尔可夫性[Markov Property]：系统的下一个状态$S_{t+1}$仅与当前状态$S_{t}$有关，而与以前的状态无关，即状态$S_{t}$是有马尔科夫性，当且仅当$P[S_{t+1} \mid S_t] = P[S_{t+1} \mid S_1,\cdots,S_t]$。$P$表示状态转移概率。

当前状态$s_t$其实是蕴含了所有相关的历史信息$S_1, \cdots, S_t$。一旦当前状态已知，历史信息将会被抛弃。简单来说，未来只和当前有关，当我们需要去决策未来时，只需要在当下的基础上去估计，因为当下状态某种程度上说已经包含之前的所有必要的历史信息。

Markov Process

Markov Property描述的是每个状态的性质，但真正有用的是如何描述一个状态序列，也就是Markov Process。

Markov Process，是具有马尔可夫(markov)性质的随机状态序列$S_1, S_2, \cdots$。由$[\mathcal{S},\mathcal{P}]$组成。其中$S$表示状态，$P$表示状态转移概率。

如下图圆圈内是状态，箭头上的值是状态之间的转移概率。class指上第几堂课，facebook可以理解看成上网玩耍，pub指去酒吧，pass指通过考试，sleep指睡觉。例如处于class1时有$0.5$的概率转移到class2，或者$0.5$的概率转移到facebook。

Markov Process Example

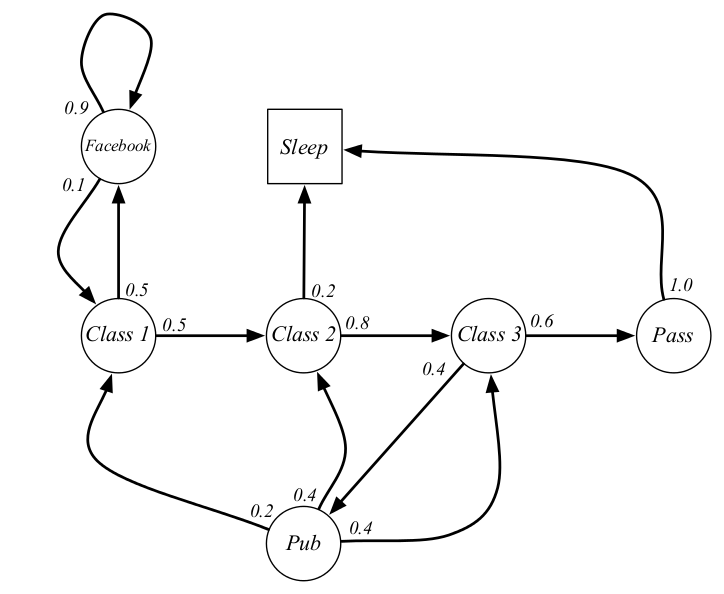
从给定的条件中，可以产生非常多的随机序列，例如C1,C2,C3,Pass,Sleep，这些随机状态的序列就是Markov Process。

Markov Reward Process

马尔可夫奖赏过程，即马尔可夫过程加上价值估计[判断一个特定的随机序列有多少累积reward]。它由$[\mathcal{S},\mathcal{P},\mathcal{R},\gamma]$组成，$\mathcal{R}$表示估计价值，或者叫即刻价值[immediate reward]，它由当前的状态决定，状态$S_t$的估计价值就是$R_{t+1}$。如下图所示，多了红色部分的Reward，但是$R$的取值只决定了immediate reward，在实际过程中需要考虑到后面步骤的reward才能确定当前的选择是否正确。

Markov Reward Process Example

基于$R$，我们引入整体价值$G_t$，定义为，

\(G_t = R_{t+1} + R_{t+2} + \cdots + R_t\) [episodic task]

\(G_t = R_{t+1} + \gamma R_{t+2} + \cdots = \sum_{k=0}^{\infty}\gamma^{k} R_{t+k+1}\) [continuing task]

回合制任务[episodic task]是指存在一个终止状态，并且所有的奖励会在这个终止状态及其之前结算清的任务。连续任务[continuing task]是指并不存在一个终止状态，即原则上可以永久地运行下去的任务，这类任务的奖励分散地分布在这个连续的一连串的时刻。为了更具一般性，我们后续使用continuing task的表达形式。

一个马尔科夫奖励过程中某一状态的价值函数为从该状态开始的马尔可夫链收获的期望，所以

\[V(S) = E[G_t \mid S_t=S]\]

$V(S)$为状态$S$的价值函数，可以用一系列马尔可夫过程然后计算其收获期望得到的。实际上$V(S)$由两部分组成，一个是immediate reward，一个是后续状态产生的discounted reward。

\[\begin{eqnarray} V(S) &=& E[G_t \mid S_t=S] \nonumber \\ &=& E[R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots \mid S_t=S] \nonumber \\ &=& E[R_{t+1} + \gamma (R_{t+2} + \gamma R_{t+3} + \cdots) \mid S_t=S] \nonumber \\ &=& E[R_{t+1} + \gamma G_{t+1} \mid S_t=S] \nonumber \\ &=& E[R_{t+1} + \gamma V(S_{t+1}) \mid S_t=S] \nonumber \\ \end{eqnarray}\]

这个推导过程相对简单，仅在导出最后一行时，将$G_{t+1}$变成了$V(S_{t+1})$。其理由是收获的期望等于收获的期望的期望。这也是针对MRP的Bellman方程。

Bellman方程，也称动态规划方程[Dynamic Programming Equation]，其核心是将某个决策问题在特定时间点的值通过来自初始选择的报酬和由初始选择衍生的决策问题的值的形式表示。针对MRP来说，某个决策问题在特定时间点的值是$V(S)$，来自初始选择的报酬是$R_{t+1}$，而由初始选择衍生的决策问题的值是$\gamma V(S_{t+1})$。如此，Bellman方程可以将一个复杂问题，不断迭代成数个小问题，进而获得“最优化”解决方案。

Markov Decision Process

马尔可夫决策过程是拥有决策能力的马尔可夫奖赏过程，马尔可夫决策过程包括$[\mathcal{S},\mathcal{A},\mathcal{P},\mathcal{R},\gamma]$和一个对应策略$\pi$，也就是说状态转移概率$P$由$\pi$决定。

此外，与之前MP和MRP不同的是，MDP拥有两个关键的值函数，分别是状态价值函数$v_{\pi}(s)$，其表示在遵循当前策略$\pi$时，处在状态$s$时的价值大小，和行为价值函数$q_{\pi}(s,a)$，其表示在遵循当前策略$\pi$时，在当前状态执行行为$a$的价值大小，其定义分别为：

\[v_{\pi}(s) = \sum_{a\in \mathcal{A}} \pi(a \mid s) q_{\pi}(s,a)\] \[q_{\pi}(s,a) = R_{s}^{a} + \gamma \sum_{s' \in \mathcal{S}} P_{ss'}^a v_{\pi}(s')\]

$v_{\pi}(s)$的定义表明在遵循策略$\pi$时，状态$s$的价值体现为在该状态下遵循某一策略而采取所有可能行为的价值按行为发生概率的乘积然后求和。$q_{\pi}(s,a)$的定义表明某一个状态下采取一个行为的价值，可以分为两部分：其一是在$s$状态下采用行动$a$的即时价值，其二是采用行动$a$后所有可能进入的新的状态的价值与其转移概率乘积的总和。可以看出，$v_{\pi}(s)$和$q_{\pi}(s,a)$之间互相依赖

对应最优的状态价值函数和行为价值函数分别表示为,

\[v^{*}(s) = \max_{\pi} v_{\pi}(s), \quad q^*(s,a) = \max_{\pi} q_{\pi}(s,a)\]

同时，其两者的最优函数同样存在依赖关系，

\[v^*(s) = \max_{a} q^*(s,a)\] \[q^*(s,a) = R_{s}^{a} + \gamma \sum_{s' \in \mathcal{S}} P_{ss'}^a v_{*}(s')\]

同样的，上面的公式说明一个状态的最优价值等于从该状态出发采取的所有行为产生的行为价值中最大的那个行为价值。下面的公式说明在某个状态$s$下，采取某个行为的最优价值由两部分组成，一部分是离开状态$s$的即刻奖励，另一部分则是所有能到达的状态$s’$的最优状态价值按出现概率求和。

Model-free MDP

首先，基于模型[Model based]的MDP， $\mathcal{P}, \mathcal{R}$是已知的，而无模型的MDP中，$\mathcal{P}, \mathcal{R}$都是未知的。也就是说我们不清楚做出了某个action之后会变到哪一个state也不知道这个action好还是不好。

更具体来说，之前公式中的$P_{ss’}^a$是未知的，所以无法直接计算值函数，必须使用采用其他的方法对当前策略进行评估，那就是后续要介绍的蒙特卡洛学习[Monte-Carlo, MC]和时序差分学习[Temporal-Difference, TD]。

Reference:

  1. 理解强化学习知识之基础知识及MDP, https://zhuanlan.zhihu.com/p/31755569
  2. 从零开始认识强化学习, https://zhuanlan.zhihu.com/p/56045177