Reinforcement Learning--Temporal-Difference
与MC一样,时序差分学习[Temporal-Difference Learning,TD]也从Episode学习,不需要了解模型本身,而是主动的是对环境做试验来得到相应”经验”。与MC不同的是,它通过学习不完整的Episode和自身的引导[bootstrapping],猜测Episode的结果,同时持续更新这个猜测。也就是说,TD方法不要求$不完整的Episode$,所以可以走一步就估算一次,也就是进行Step-Based的强化学习。因为可以克服诸多限制,TD方法是强化学习理论中最核心的内容,是强化学习领域最重要的成果。
Bootstrapping可以根据中间状态估计当前可能获得的回报,并且更新之前状态能获得的回报。比如,一个episode包括10个step[或者说经历10个state],TD可以只采样第一个和第二个step,然后就可以估计出整个episode的回报。因此,它不需要走完一个episode的全部流程获得回报再更新。估计整个episode的回报的具体做法,一种是根据已经存在的状态转移概率和回报函数进行计算,也就是知道$\mathcal{P}_{ss’}^a$[这个比较少见],另一个在model free的情况下,还是要根据类似MC的采样方式进行计算[有点像套娃,一个估计值是基于另外一批估计值,这就是带来了准确度的隐患]。
类似MC方法,TD方法的价值更新函数公式为:
\(V(S_t) \leftarrow V(S_t) + \alpha(G_t - V(S_t))\) [MC]
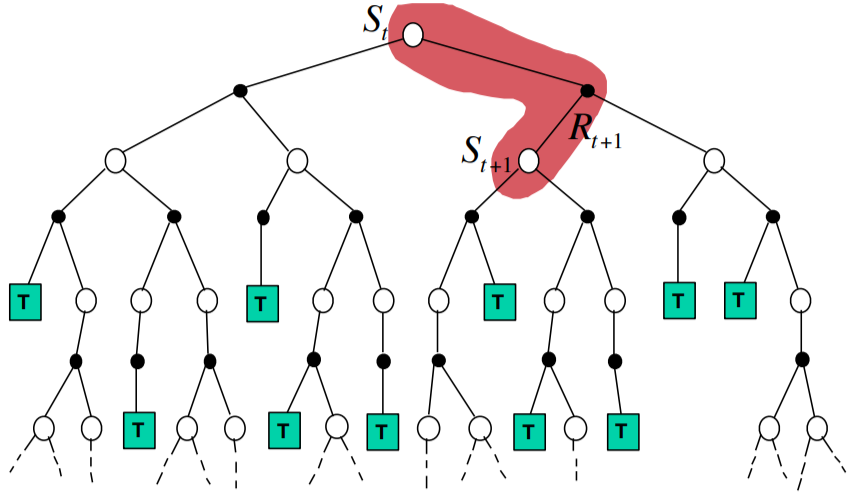
\(V(S_t) \leftarrow V(S_t) + \alpha(R_{t+1} + \gamma V(S_{t+1}) - V(S_t))\) [TD]
其中$G_t$是MC的真实回报,而$R_{t+1} + \gamma V(S_{t+1})$对应$G_t$是TD中对于回报的估计,这是因为TD算法不要求完整的执行一次episode,所以只能估计。估计方式也很简单$R_{t+1}$代表当前的直接回报,$\gamma V(S_{t+1})$则是对下一状态的价值函数估计。区别如下图所示,
| MC | TD |
|---|---|
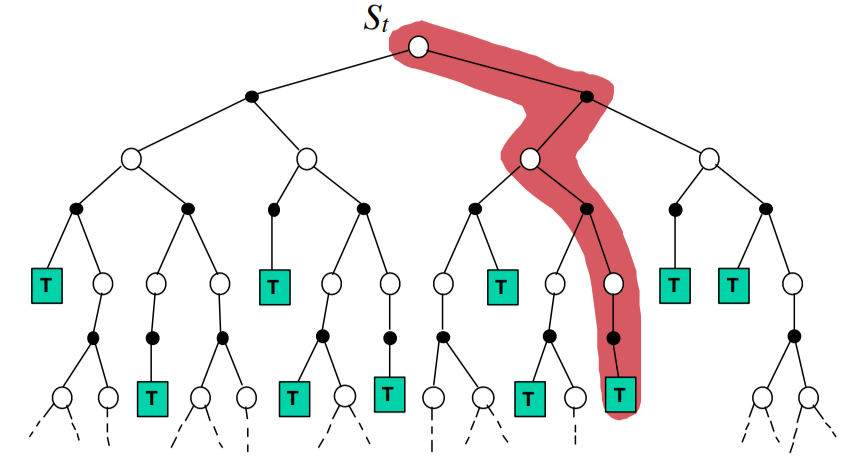 |
 |
V-function vs Q-function
之前介绍MDP的时候说过MDP有两个价值函数,V-function[状态价值函数]和Q-function[行为价值函数]。在model free的环境下,无法知道当前状态的所有后续状态及其状态转移概率,进而无法确定在当前状态下采取怎样的行为更合适。如此以来,任何含有$P_{ss’}^a V(s)$的方法都无法使用,而解决这一问题的方法就是使用行为价值$Q(s,a)$来代替状态价值$V(s)$:
\(\pi^{*}(s) = \underset{a \in \mathcal{A}}{\operatorname{arg max}} (\mathcal{R}_{s}^{a} + \mathcal{P}_{ss'}^{a} V(s'))\) [V-function]
\(\pi^{*}(s) = \underset{a \in \mathcal{A}}{\operatorname{arg max}} Q(s, a)\) [Q-function]
直观上看,V-function依赖明确的下一状态$s’$,但是Q-function只需要根据当前状态$s$就可以确定下一个动作,从而进行策略评估和提升。
SARSA
SARSA是一个经典TD算法,其得名就是流程$S \rightarrow A \rightarrow R \rightarrow S \rightarrow A$的缩写。一言以蔽之,在SARSA算法的眼中,在状态$S$下,要想把动作$A$的估值$Q(S, A)$计算准确,就需要研究序列$S \rightarrow A \rightarrow R \rightarrow S’ \rightarrow A’$,因为也属于TD方法,其价值函数及其更新方式:
\[Q(S, A) \leftarrow Q(S, A) + \alpha(R + \gamma Q(S', A') - Q(S,A))\]两个参数$\alpha$和$\gamma$的作用和之前类似,$\alpha$的值越小,说明”记忆”的周期越长,也可以说,对于估值,用来计算平均的周期越长。$\gamma$是discount,它表示对于长期回报的好恶。其值越大,说明算法对远期的回报越重视,越倾向于把它们的得失算在当前决策的头上;值越小,说明算法越无视长期回报;如果是0,则表示指考虑当前回报。

Pros & Cons
SARSA算法是model-free,而且不要求环境基于MDP。同时,SARSA算法的估值和反馈速度比较快,可以走一步就进行一次反馈,而需要像MC方法那样,必须等一个完整的Episode结束才能给出反馈。
不过,在实验中,尤其在简单的场景中,SARSA算法的收敛速度不如下面的Q-Learning算法快。
Q-Learning
Q-Learning算法也是另一种经典的TD算法。而且,Q-Learning算法是强化学习中最为有效最具普适性的算法。尽管从名字上看不出它是如何工作的,但它仍然是一个TD算法,并且是Off-Policy的[这一点与SARSA不同,SARSA是On-Policy的]。
其价值函数及其更新方式和SARSA非常相似,
\(Q(S, A) \leftarrow Q(S, A) + \alpha(R + \gamma Q(S', A') - Q(S,A))\) [SARSA]
\(Q(S, A) \leftarrow Q(S, A) + \alpha(R + \gamma \max_{a'} Q(S', A') - Q(S,A))\) [Q-Learning]
其区别是max,Q-Learning算法对$Q(S, A)$同样参考了其后所能转移到的所有状态$S’$可能做的所有动作$A’$,并认为其中的最大估值才是当前$Q(S, A)$的估值。
其实核心区别就是off-policy vs on-policy,SARSA选择action的空间只是根据当前的策略,也就是从当前策略而产生的所有action中选择。而Q-Learning的,并不只是根据当前的策略,而是从所有已知的策略而产生的action中选择价值最max的一个。所以,Q-Learning比SARAS更为激进。这就类似下棋,SARSA只是根据棋手根据自己的想法落子,然后不断学习。而Q-Learning就像一个棋手下棋时手边还有很多本棋谱可以随时查阅,然后选择最好的落子方式。
Pros & Cons
Q-Learning因为使用max进行估值计算,容易在比较简单的环境中发现最优路径或者找到最好的策略。
但是,Q-Learning几乎无法实现输出动作为连续值的场景。其实,不仅Q-Learning算法存在这样的缺陷,SARSA算法也存在这样的缺陷。
最后,对一个状态,要想估算它的价值,尚且需要使用数学期望值这样的概念,通过多次测量取平均值。因此,单纯以最大值来做评价是有失偏颇的,也就会产生过估计[overestimating]。但这只是有暂时性的估值过高的问题而已,并不妨碍Q-Learning是一个优秀的强化学习算法。
Reference:
- 理解强化学习知识之解决无模型的MDP, https://zhuanlan.zhihu.com/p/32161274
- Sutton, Richard S., and Andrew G. Barto. Reinforcement learning: An introduction. MIT press, 2018.
- 高扬,叶振斌,白话强化学习与PyTorch