Reinforcement Learning--REINFORCE
基于价值函数的方法就是通过计算每一个状态动作的价值[基于$V(s)$或者$Q(s,a)$],然后选择价值最大的策略执行。其实,这是一种比较间接的做法,因为我们最终要的是最优的策略。
Policy Gradient
策略梯度是一种直接的方式。也就是说直接参数化策略本身,然后优化参数达到优化策略的目的:
\[\pi_{\theta} = P[a \mid s, \theta]\]上式将策略函数理解成参数化的策略函数$\pi_{\theta}$。策略函数确定了在给定的状态$s$和一定的参数$\theta$下,采取任何可能行为的概率。我们要做的是利用参数化的策略函数,通过调整参数来得到一个较优策略,遵循这个策略产生的行为将得到较多的奖励。具体的机制是设计一个目标函数,对其使用梯度上升[Gradient Ascent]算法优化参数以最大化奖励。之前用线性和非线性的方式对价值函数进行逼近求解,那同样的,也可以利用线性或非线性对策略进行求解。
引入参数化策略的目的是为了解决大规模问题。在大规模的问题里,把每一个状态严格的独立出来,并指出某个状态下应该执行某个行为是很困难的甚至是不可能的。因此我们需要参数化,用少量的参数来合理近似实际的函数[这个思路和使用线性和非线性函数拟合价值函数异曲同工]。在很多方面,策略梯度有其优点和缺点:
Target Function
所有的最优策略有相同的最优价值函数,也就是找到最优值函数,就能对应找到最好策略。要的到最优的策略就是要尽可能获得更多的奖励。而将策略表达成带参数$\theta$的目标函数,有如下几种形式:
Start Value: 在能够产生完整episode的环境下,也就是agent可以到达终止状态时,我们可以用这样一个值来衡量整个策略的优劣:从某状态$s_1$直到终止状态,agnet获得的累计奖励。这个值称为start value。其表明:如果个体总是从某个状态$s$开始,或者以一定的概率分布从$s$开始,那么从该状态开始到episode结束,agent将会得到多少最终奖励。这个时候算法真正关心的是找到一个策略,当把agent放在这个状态$s$让它执行当前的策略时,能够获得最大的start value。
\[J(\theta) = V^{\pi_{\theta}}(s)\]Average Value: 对于连续环境,不存在一个开始状态而且停止状态也不固定,这个时候可以使用average value。其表达:考虑agent在某时刻处在某状态下的概率,也就是agent在该时刻的状态分布,然后针对每个可能的状态计算从该时刻开始一直持续与环境交互下去能够得到的奖励并求和。其中,$d^{\pi_{\theta}}$是在当前策略下马尔科夫链的关于状态的一个静态分布
\[J(\theta) = \sum_{s} d^{\pi_{\theta}}(s) V^{\pi_{\theta}}(s)\]Average Reward per time-step: 使用每一个时间步长在各种情况下所能得到的平均奖励,也就是说在一个确定的时间步长里,agnet出于所有状态的可能性,然后每一种状态下采取所有行为能够得到的即时奖励,所有奖励按概率求和的方式得到
\[J(\theta) = \sum_{s} d^{\pi_{\theta}}(s) \sum_{a} \pi_{\theta}(s,a) R_{s}^{a}\]Optimization

所以,现在得到所有形式的目标函数所对应的策略梯度是一样的,注意这里有两个部分组成,一个是策略函数的$log$形式,一个是引导奖励。第一部分是参数化直接得到的,第二部分可以直接用即时奖励来计算,也可以用值函数近似。
REINFORCE
假设$\pi_{\theta}$是可微的,那就像在优化值函数,只是这里$\theta$不是值函数的参数,而是policy的参数,用目标函数对参数求导。下面给出具体基于蒙特卡洛的策略梯度的REINFORCE算法伪代码:
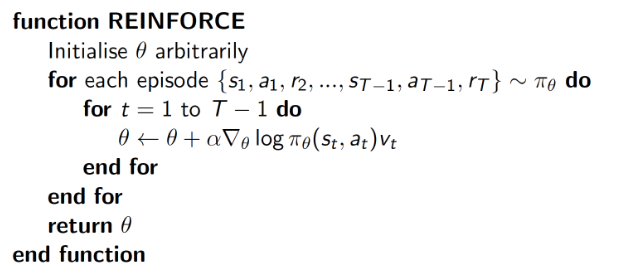
Reference:
- 理解强化学习知识之策略梯度, https://zhuanlan.zhihu.com/p/32438022
- Richard S. Sutton and Andrew G. Barto. Reinforcement learning: An introduction. MIT press, 2018.
- 高扬,叶振斌,白话强化学习与PyTorch